Domov Blog~~Podrobný sprievodca k úplnému addéru~~

~~na 2024/05/10~~ ~~600~~

Podrobný sprievodca k úplnému addéru

V oblasti digitálnej elektroniky a počítačového inžinierstva Adders predstavujú jeden z najdôležitejších stavebných blokov, ktoré sú kľúčové v konštrukcii a funkčnosť zložitejších aritmetických obvodov.Ako integrálne komponenty aritmetickej logickej jednotky (ALU), Adders uľahčujú početné výpočtové operácie, od základných aritmetických po zložité logické úlohy potrebné pre operácie systémov.Ich dizajn, ktorý sa môže líšiť v závislosti od jednoduchých polovičných adderov po zložitejšie úplné doplnky, hrá rozhodujúcu úlohu pri zvyšovaní účinnosti a rýchlosti spracovania v digitálnych systémoch.Tento článok sa ponorí do podrobnej architektúry a funkčných nuancií rôznych typov addérov, čo ilustruje ich kritickú úlohu v modernej výpočtovej technológii a skúma ich prevádzkovú logiku, obvody a aplikácie v širšom kontexte digitálneho logického návrhu.

Katalóg

1. Čo je to adder?

2. Polovica

3. Celá adder

4. Tabuľka pravdy s úplným adderom

5. Charakteristické rovnice úplného addéra

6. Implementácia úplného obvodu adder

7. Výhody a nevýhody úplných pridružení

8. Aplikácie úplných addárov v digitálnej logike

9. Príklady implementácií úplných adderov

10. Záver

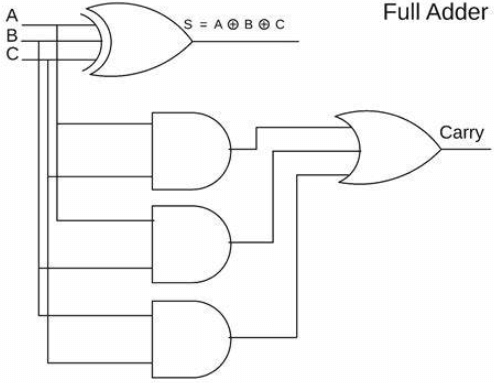
Obrázok 1: Celá adder

Čo je to adder?

Adder je základnou súčasťou dizajnu elektronického inžinierstva a digitálnej logiky a hrá ústrednú úlohu v zložitejších počítačových systémoch.Ako súčasť aritmetickej logickej jednotky (ALU) sa kupok zaoberá rôznymi základnými počítačovými úlohami.Efektívnosť a výkon celého procesora sú priamo ovplyvnené návrhom a funkčnosťou addéru.

V procesore sa adder používa nielen na základné aritmetické operácie, ako je pridanie a odčítanie, ale tiež sa zapája do širšej škály logických operácií.Napríklad pri spustení programov potrebuje procesor často vypočítať nové adresy pamäte.Zvyčajne sa to robí pridaním alebo odpočítaním od aktuálnej adresy - úlohy, ktorú vykonáva adder.Ovládajú počet iterácií slučky a celkový tok zvyšovaním a znižovaním počítadiel.V zložitejších aplikáciách, ako je indexovanie tabuliek, pridania rýchlo lokalizujú údaje výpočtom kompenzácií.Je to dôležité pre systémy riadenia databáz, konštrukciu kompilátorov a rozsiahle spracovanie údajov.Adders sú tiež kľúčom k implementácii určitých mapovacích techník vo viacúrovňových vyrovnávacích systémoch, pomocou aritmetických operácií na určenie polohy údajov v vyrovnávacej pamäti, čím sa optimalizuje efektívnosť prístupu.

Technologicky sú pridania implementované prostredníctvom rôznych návrhov obvodov vrátane paralelných, sériových a dodávateľov potrubia.Paralelné doplnky sú uprednostňované pre ich schopnosť zvládnuť viac číslic súčasne, vďaka čomu sú vhodné pre scenáre, ktoré si vyžadujú rýchly výpočet.Na druhej strane sériové pridania spracúvajú cyklus jedného bit za hodiny a sú ideálne pre prostredie obmedzené na zdroje alebo nízkoenergetické prostredie.Pridávače potrubia rozdeľujú proces pridávania do niekoľkých etáp, z ktorých každá má súčasť časti pridania.Táto konštrukcia výrazne zvyšuje rýchlosť výpočtu, najmä vo vysoko výkonných výpočtových prostrediach.

Napoly

Obvod s polovičnou váhou je základný stavebný blok v digitálnej elektronike, ktorý je špeciálne navrhnutý tak, aby pridal dve binárne číslice.Tento obvod tvorí základ úplného kladenia a je kľúčom k pochopeniu zložitejších návrhov logických obvodov.V polovici kladenia existujú dva primárne vstupy označené A a B, ktoré predstavujú Auguend a dodatok.Toto nastavenie umožňuje vypočítať súčet a vykonávať výstup bez potreby prenosného vstupu z predchádzajúcich výpočtov.

Jadro polovičnej sadzby pozostáva z dvoch logických brán: brána XOR a brána.Brána XOR je zodpovedná za generovanie výstupu súčtu.Pôsobí pod jednoduchým pravidlom, kde výstup 1, ak je iba jeden z jeho vstupov 1;V opačnom prípade na druhej strane vystupuje a brána a brána zvládne výstup prepravy.Vytvára 1 iba vtedy, keď sú oba vstupy 1, čo je dokonale v súlade so základnými požiadavkami binárneho pridávania.

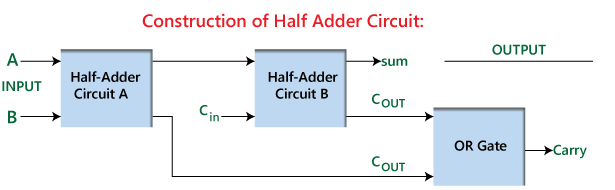
Obrázok 2: Konštrukcia polovičného kupca

Tento efektívny a priamy dizajn umožňuje polovičnému kladeniu nielen vykonávať základné binárne pridanie nezávisle, ale tiež slúžiť ako stavebný blok na vytvorenie úplného addéra.Celá adder je skonštruovaná kombináciou dvoch polovičných pridaní s ďalšou alebo bránou.V tomto nastavení preberá prvá polovica adder na počiatočnú úlohu pridávania, ktorá generuje predbežnú sumu a prepravuje sa.Druhá polovica kupca potom spracuje prepravu od prvého spolu s ďalším vstupom prepravy.Nakoniec alebo brána zlúčia tieto dva výstupy, aby sa vytvoril konečný výstup.Toto usporiadanie zvyšuje funkčnosť adderu, čo mu umožňuje zvládnuť zložitejšie viac-bitové pridávajúce úlohy, ktoré predstavuje rozšírenú aplikáciu a dôležitosť polovičných pridaní pri návrhu digitálnych obvodov.

Plné

Celý adder je pokročilý komponent v digitálnej logickom dizajne, ktorý je vybavený na zvládnutie pridania troch jedno-bitových binárnych vstupov, bežne označených ako A, B a prenášanie (CIN).Táto konštrukcia umožňuje úplnému kladeniu efektívne spracovať komplexné binárne prírastky začlenením prenosu z predchádzajúcich výpočtov nižších rádov do jednej operácie.

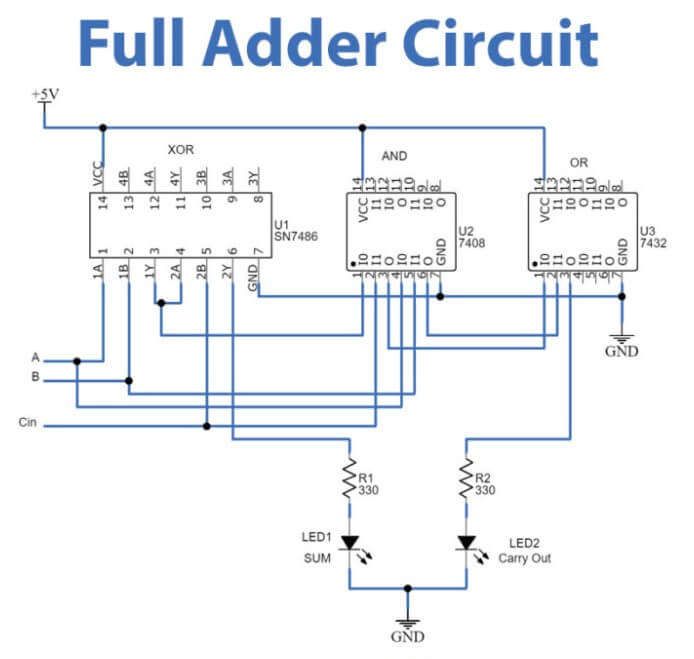
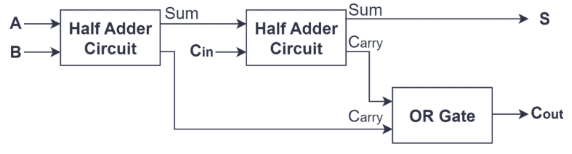
Obrázok 3: Obvod s úplným adderom

Funkčne môže kompletný kalpón na výstup dvojciferného súčtu, čo znamená, že jej výstup sa môže pohybovať od 0 do 3 a môže tiež vyrobiť vykonávanie (cout).Deje sa to preto, že keď sú všetky vstupné bity nastavené na 1 (a = 1, b = 1, cin = 1), výstup sumy bude 1 (predstavujúci binárny 01) a vygeneruje sa vykonanie 1, čo naznačuje, že naznačuje, že to znamenáĎalší prenos je potrebné odovzdať na ďalší vyšší bit.

Štrukturálne sa celá adder všeobecne pozostáva z dvoch polovičných doplnkov a jednej alebo brány.Adder v prvej polovici prijíma vstupy A a B, ktorý generuje počiatočný súčet a signál prenášania.Táto počiatočná suma sa potom kŕmí spolu s prenosom (CIN) do druhej poloviceadša.Úlohou druhej polovice Adder je pridať túto sumu z prvej polovice kladenia do CIN, čím sa vytvorí ďalšia suma a nový výstup.Súčasne sa výstup z prvej polovice kupca a výstup z druhej polovice kupca zlúčia cez alebo bránu, čo vyvrcholí konečným vykonaním (cout) plného kladenia.Návrh tejto štruktúry zaisťuje, že úplný adder efektívne zvláda šírenie nosičov navyše, čo je ideálna na vykonávanie viac bitových binárnych dodatkov.Návrh úplného adderu teda nielen urýchľuje spracovanie údajov a zvyšuje účinnosť, ale tiež zjednodušuje zložitosť implementácie hardvéru prostredníctvom priamej kombinácie logických brán, čím sa stane nevyhnutnou komponentom vo viaccifernom pridaní a aritmetickej logickej jednotke (ALU.).

Parametre	Napoly	Plné
Opis	Half Adder je kombinácia logika Obvod, ktorý pridáva dve 1-bitové číslice.Polovica vstupy.	Celá adder je kombinácia logika Obvod, ktorý vykonáva operáciu pridania na troch jedno-bitových binárnych číslach. Celá adder vytvára súčet troch vstupov a hodnoty prenosu.
Predchádzajúce nosenie	Predchádzajúce nosenie sa nepoužíva.	Používa sa predchádzajúce nosenie.
Vstupy	V polovici kladenia existujú dva vstupné bity (A, B).	V plnom prúde sú tri vstupné bity (A, B, C_v).
Výstupy	Generovaný výstup je z dvoch bitov sumy a niesť zo vstupu 2 bitov.	Generovaný výstup je z dvoch bitov sumy a noste zo vstupu 3 bitov.
Použitý ako	Obvod s polovičnou sadou sa nemôže použiť v Rovnakým spôsobom ako obvod s úplnou sadou.	Na mieste je možné použiť celý obvod s adderom Polovičného obvodu kupolov.
Funkcia	Je jednoduché a ľahké implementovať	Dizajn úplného addéra nie je taký Jednoduché ako polovičné kladenie.
Logické vyjadrenie	Logický výraz pre polovičnú klientu je: S = a⊕b;C = a*b.	Logický výraz pre plnú adder je: S = a⊕b⊕cin;C_vyčlenený= (ab)+(c_v(a⊕b)).
Logické brány	Pozostáva z jednej bývalej alebo brány a jednej a brána.	Pozostáva z dvoch bývalých alebo dvoch a Gates, a jedna alebo brána.
Žiadosti	Používa sa v kalkulačkách, počítačoch, Digitálne merací zariadenia atď.	Používa sa vo viacerých bitoch, digitálne spracovateľy atď.
Alternatívny názov	Neexistuje žiadny alternatívny názov pre polovicu adder.	Celá adder je známa aj ako zvlnenie adder.

Graf 1: Rozdiel medzi polovičnou kladkou a úplným adderom

Úplná tabuľka pravdy s adderom

Tabuľka pravdy úplného addéra je kľúčom k pochopeniu jeho prevádzkovej logiky a podrobne opisuje presný vzťah medzi binárnymi vstupnými kombináciami a ich zodpovedajúcimi výstupmi.Táto tabuľka demonštruje všetky potenciálne vstupné scenáre a ich výsledky, vďaka čomu je nevyhnutným nástrojom pri navrhovaní a overovaní digitálnych logických obvodov.Celá adder spracováva tri vstupy: A, B a prenos (CIN), z ktorých každý môže byť buď 0 alebo 1. To má za následok osem možných kombinácií vstupov.

Pre každú z týchto kombinácií patrí výstupy z celého addéru súčet (súčet) a vykonanie (cout).Súčet je pridanie modulo-2 (operácia XOR) troch vstupov-A, B a CIN.K vykonávaniu dochádza, keď sú najmenej dva vstupné bity 1. Odráža to schopnosť úplného kladenia zvládnuť prenos v sekvenčných operáciách pridávania, čím sa zabezpečuje presnosť pri výpočtoch vyšších bitov.

Na ilustráciu zvážte vstupný scenár, v ktorom sú všetky vstupy 0 (a = 0, b = 0, c-in = 0).Výstupná suma bude 0 a nosenie bude tiež 0, čo naznačuje, že na správu nie je žiadna dodatočná suma ani prenášať.Ak je iba jeden vstupný bit 1, napríklad a = 1, b = 0, c-in = 0, výstupná suma bude 1 bez prenosu, čo ukazuje, že nie je potrebné prenášať prenos na vyšší bit.Keď sú dva vstupné bity 1, ako a = 1, b = 1, c-in = 0, výstupná suma je 0 (pretože 1+1 sa rovná 2 v binárnom a modulo-2 viedlo k 0), ale prenášanieOut je 1, čo naznačuje prenos, ktorý je potrebné preniesť na ďalší vyšší bit.Najkomplexnejší scenár sa vyskytuje, keď sú všetky tri vstupné bity 1 (a = 1, b = 1, c-in = 1);Výstupná suma je 1 a existuje vykonanie 1, čo naznačuje, že riadenie nosenia sa môže vyžadovať aj pri ešte vyšších bitoch.

A	B	C_v	Siež	C_vyčlenený
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Graf 2: Tabuľka pravdy s úplným adderom

Charakteristické rovnice úplného addéra

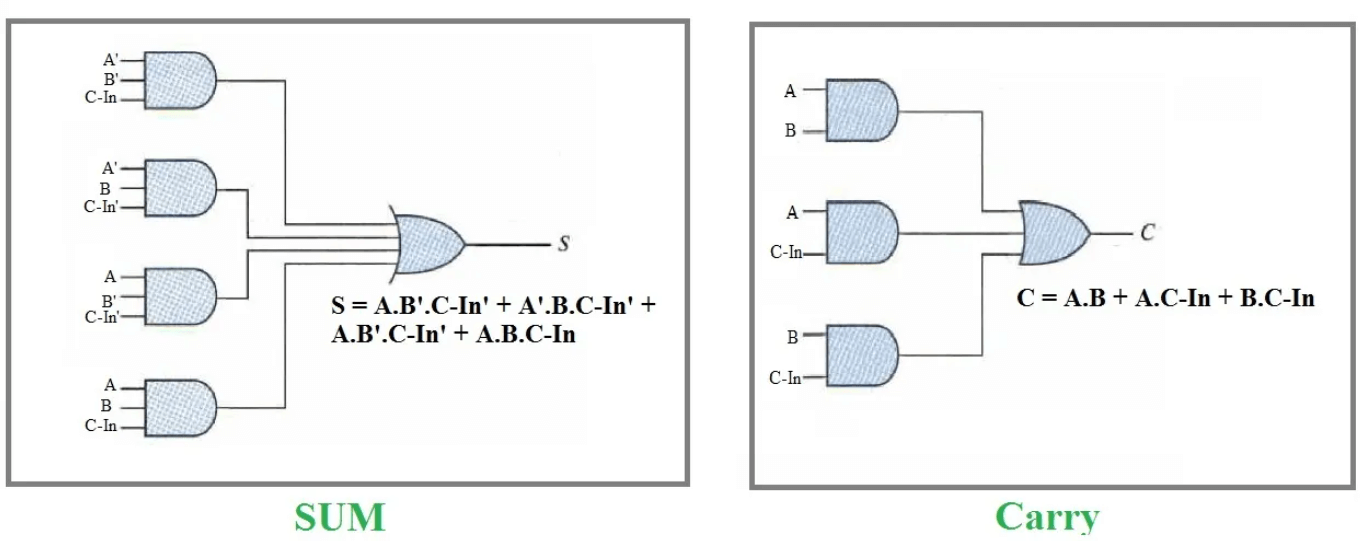
Pochopenie úplného addéra zahŕňa rozlíšenie jeho funkčnosti pomocou tabuľky pravdy, kde rôzne kombinácie vstupných hodnôt A, B a C-in vedú k súčtu výstupov a cout.Na pochopenie operácie zjednodušujeme logické rovnice krok za krokom.

Logický výraz pre sumu

Rovnica začína odlišnými prípadmi, keď sa súčet rovná 1:

• „B“ CIN + A 'B CIN' + A B 'CIN' + AB CIN

Túto rovnicu sa dá kondenzovať zoskupením podmienok s CIN a bez CIN:

• CIN (A 'B' + AB) + CIN '(A' B + A B ')

Toto zjednodušenie vedie k ľahšiemu forme implementu:

• CIN XOR (A XOR B)

Táto reprezentácia ukazuje, že výstup sumy je v podstate operáciou XOR medzi A, B a CIN, ktoré zachytáva základné správanie binárneho pridávania, kde súčet prepína na základe nepárneho počtu z nich.

Logika pre cout

Počnúc podmienkami, kde sa generuje prenos:

• A 'B CIN + A B' CIN + AB C-in ' + AB CIN

Zjednodušenie rovnice identifikujeme výrazy, ktoré bežne zahŕňajú generovanie prenosu:

• ab + b cin + cin

Pri hľadaní inej metódy na implementáciu Cout je možné reorganizovať rovnicu:

• AB + CIN + B C-in (A + A ')

To rozširuje a rekombiníny zachytáva všetky scenáre, v ktorých sú najmenej dva vstupy 1:

• AB CIN + AB + C-in + A 'B CIN

• ab (1 + cin) + c-in + a 'b cin

• AB + C-in (b + b ') + a' b cin

• AB + A B 'CIN + A' B CIN

• AB + CIN (A 'B + A B')

Konečný kompaktný formulár pre cout:

• AB + CIN (XOR B)

Táto verzia vykonávanej rovnice ukazuje, ako sa vyrába cout buď vtedy, keď sú A aj B 1, alebo keď je jedným z A alebo B 1 spolu s prenosom, čím sa zapuzdruje logika potrebná na riadenie šírenia pri viacBit binárne pridanie.Táto efektívna logika je obzvlášť užitočná na implementáciu efektívnych digitálnych obvodov.

Obrázok 4: Rovnice úplného addéra

Implementácia úplného obvodu adder

Implementácia úplného obvodu adder zahŕňa starostlivo zostavenie dvoch polovičných pridaní a brány na vytvorenie zariadenia schopného efektívneho zvládnuť pridanie troch jedno-bitových binárnych vstupov.Toto usporiadanie optimalizuje zložitosť obvodu a zaisťuje efektívne aj presné výpočty.

Na začiatok má prvá polovica kupca dva primárne binárne vstupy, A a B, ktoré sú hlavnými číslicami, ktoré sa majú pridať.Jeho kľúčovou úlohou je vypočítať súčet a počiatočné prevedenie týchto dvoch čísel.Tu prvá polovica adder prináša dva výsledky: počiatočná suma (SUM1) a počiatočný prenos (prenášanie1).SUM1 je odvodený z operácie XOR A a B, čo naznačuje, či má celková suma nepárny počet 1.Prenášanie1, výsledok a prevádzka medzi A a B, naznačuje, či sú obe číslice 1, čo si vyžaduje prepravu k ďalšiemu vyššiemu bitke.

Ďalej sa k procesu pripojí druhá polovica kladu.Ako jej vstupy používa výstup Sum SUM1 a tretí vstupný CIN (prenášanie z predchádzajúceho výpočtu).Druhá polovica kupca vytvára dva výstupy: výsledok konečného súčtu (SUM2) a sekundárny nosenie (prenášanie2).SUM2, ktorý je výsledkom XOR SUM1 a CIN, predstavuje konečný súčet troch vstupov, pričom zobrazuje agregované binárne prírastok.Prenášanie2, vychádzajúci z a prevádzky medzi SUM1 a CIN, naznačuje prenos generovaný týmito komponentmi.

Full Adder Circuit with Using Two Half Adder

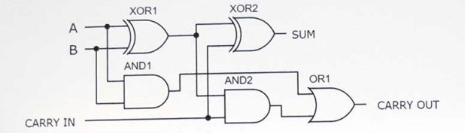
Obrázok 5: Celý obvod adder s použitím dvoch polovičných addérov

Nakoniec, aby ste dokončili dizajn úplného addéra, je potrebná brána alebo brána, aby zvládla výstupy prepravy1 a prepravy2 z oboch polovičných pridaní.Táto alebo brána zaisťuje, že akýkoľvek prenos generovaný počas výpočtov je správne postúpený do konečného výstupu.Preto je konečný výstup z plného adder (Cout) alebo výsledkom prenášania1 a prenášania2.Zahrnutie tohto alebo brány zaručuje, že všetky potenciálne prepravy sa presne vypočítajú a sprostredkujú na ďalšiu úroveň do viac-bitových prídavkových operácií, čím sa zabezpečuje integrita aritmetickej prevádzky vo viacerých bitoch.

Výhody a výzvy úplných addárov v digitálnej logike

Úplní pridaní zohrávajú nevyhnutnú úlohu pri dizajne digitálnej logiky a ponúkajú početné výhody, vďaka ktorým sú nevyhnutné v rôznych scenároch výpočtových počítačov a spracovania údajov.Medzi ich primárne výhody patrí pozoruhodná flexibilita, rýchle rýchlosti spracovania a efektívne riadenie nosenia.Vďaka týmto znakom sú úplné pridania ideálnymi na vykonávanie zložitých aritmetických operácií a logických funkcií, najmä v aplikáciách vyžadujúcich postupný multi-bitový prírastok.

Výhody

Flexibilita: Úplné doplnky vynikajú v ich schopnosti spracovať viacero binárnych vstupov (A, B a CIN) súčasne.Môžu sa tiež rozšíriť do väčších polí adder, aby sa zvládli dlhšie binárne čísla.Táto škálovateľnosť je dôležitá pre budovanie vysokovýkonných aritmetických logických jednotiek (Alus), ktoré musia vykonávať zložité multi-bitové aritmetické a logické operácie.

Rýchlosť: Vďaka svojej internej architektúre paralelného spracovania môžu úplné pridania dokončiť pridanie všetkých vstupov do jedného hodinového cyklu a zároveň určiť výstupy.Táto schopnosť podporuje prevádzku kontinuálneho pridávania a je nevyhnutná pre spracovanie údajov v reálnom čase v moderných mikroprocesoroch a vysokorýchlostných výpočtových zariadeniach.

Nevýhody

Úplné pridania však tiež predstavujú pozoruhodné nevýhody:

Zložitosť v návrhu a implementácii: Úplné pridania zahŕňajú viac logických brán a viacúrovňové šírenie nosenia, vďaka čomu je ich dizajnový komplex.Táto zložitosť nielen zvyšuje výrobné náklady, ale môže tiež ovplyvniť spoľahlivosť obvodov.

Problémy s oneskorením šírenia: Prenesenie šírenia môže prejsť niekoľkými logickými bránami, z ktorých každá pridáva jej oneskorenie.To môže obmedziť celkovú výpočtovú rýchlosť počas rozsiahlych operácií, najmä v rozsiahlych počítačových systémoch a pri návrhu integrácie s veľmi veľkým rozsahom (VLSI) a vysokorýchlostných procesorov.Oneskorenie sa môže stať významným problémom výkonu.

Na zmiernenie týchto problémov inžinieri nepretržite skúmajú efektívnejšie návrhy obvodov.Medzi stratégie patrí použitie rýchlejších technológií logickej brány, optimalizácia rozloženia obvodov na skrátenie dĺžiek ciest a vývoj pokročilých technológií, ako sú Adders Adders, aby sa minimalizovali oneskorenia pri šírení prenášania.

Aplikácie úplných addárov v digitálnej logike

Úplné doplnky sa vo veľkej miere používajú v digitálnej logike, ocenení za svoju flexibilitu a efektívnosť, čo ich robí ústredným prvkom pre množstvo úloh výpočtových a údajov o spracovaní údajov.Ich aplikácia sa rozprestiera od základných aritmetických operácií k komplexnému spracovaniu signálu a riadenia systému.Tu je podrobný pohľad na niektoré kľúčové oblasti, v ktorých sú úplní pridaní.

Aritmetické obvody

Jedným z najpriamejších použití úplných pridaní je v aritmetických obvodoch, kde vykonávajú binárne pridanie.Obzvlášť rozhodujúce vo viac-bitovom pridávaní čísla, úplní pridaní riadia dlhšie binárne sekvencie prostredníctvom kaskádovania.V tomto usporiadaní každá úplná adder spracováva pridanie svojej bitovej polohy a prenášanie z dolného bit, potom prechádza novým prenosom do úplného kupca s vyšším bitom.Táto kaskáda umožňuje komplexné viac-bitové pridávanie v celom rozsahu číslic.

Spracovanie údajov

Úplné pridania zohrávajú tiež kľúčovú úlohu pri pokročilých úlohách spracovania údajov, ako je spracovanie digitálneho signálu (DSP) pre filtrovanie a Fourierové transformácie, kde sú potrebné presné a rýchle aritmetické operácie.Okrem toho v oblasti informačnej bezpečnosti vrátane algoritmov detekcie a detekcie chýb a korekcií, ako sú kontrola parity a generovanie kódu cyklického redundancie (CRC), sú úplné pridania rozhodujúce pre vykonávanie základných bitových operácií.

Pult

V digitálnych počítadlách sú úplné doplnky nevyhnutné na implementáciu funkcií prírastkov aj poklesov, najmä v modulárnych a synchrónnych počítadlách.Presne spravujú nosenie a požičiavanie, aby sa zabezpečilo presné počítanie.

Multiplexory (MUX) a demultiplexory (DeMUM)

V multiplexoroch a demultiplexéroch zohrávajú úplné pridania rozhodujúcu úlohu pri výbere kanálov a distribúcii údajov.Zúčastňujú sa na logike, ktorá určuje, ktoré kanály sa používajú na vstup a výstup údajov, čím sa rozhodujú na základe logických riadiacich signálov.

Pamäťová technológia

Pri adrese pamäte pomáhajú úplné pridania generovať signály adresy pre dynamické prístupy k umiestneniu pamäte.Toto je obzvlášť dôležité v dynamickej pamäti náhodného prístupu (DRAM) a ďalších úložných systémoch, kde úplní pridaní podporujú komplexné výpočty adries na zvýšenie účinnosti prístupu do pamäte.

Aritmetické logické jednotky (ALU)

Nakoniec, ako základné komponenty aritmetických logických jednotiek v mikroprocesoroch a procesoroch digitálneho signálu sú úplné pridania rozhodujúce.ALU spracováva všetky aritmetické a logické operácie, pričom úplné pridania zabezpečujú spracovanie údajov rýchlo aj presne.

Príklady úplných implementácií adder

Úplné doplnky je možné skonštruovať pomocou rôznych logických brán a konfigurácií.Tu skúmame štyri rôzne implementácie, ktoré zdôrazňujeme ich nastavovacie a prevádzkové nuansy.

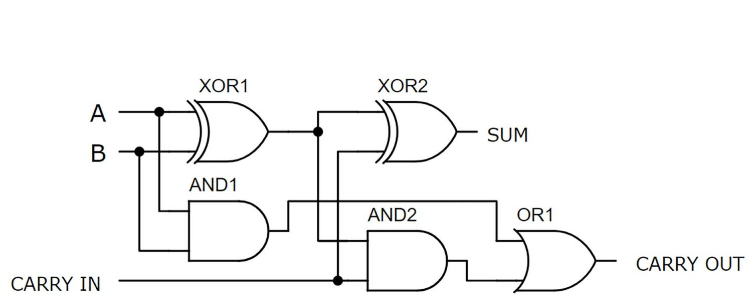
Plné adder postavené s XOR a a alebo brány

Full Adder Built with XOR, AND, and OR Logic Gates

Obrázok 6: Celý adder postavený s XOR a a alebo logické brány

Tento príklad predstavuje úplnú adder postavenú na dosku pomocou diskrétnych tranzistorov.Konfigurácia obsahuje päť logických brán: dve brány XOR, dve a brány a jedna alebo brána, ktorá vyžaduje celkom 21 tranzistorov.Vstupy A a B sú pripojené k ľavej hornej časti dosky, ktoré dostávajú napájanie A +5V.Tieto vstupy sú ovládané pomocou dvoch prepínačov.Dve LED v ľavom hornom rohu označujú stavy vstupov A a B, zatiaľ čo dve LED na pravej strane zobrazujú výstupy.Odpory použité v obvode sú všetky 2,2 k ohmov.Ak sú vstupy A a B zapnuté a prenos je vypnutý, výstup ukazuje binárnu hodnotu 10, čo predstavuje súčet 2 (1 + 1 + 0 = 10).Brány XOR, postavené z prvých 12 tranzistorov, zvládajú primárne zhrnutie, zatiaľ čo spodná polovica dosky obsahuje a alebo brány na prenos operácií, farebne kódované zapojenie zvyšuje čistotu a riešenie problémov.

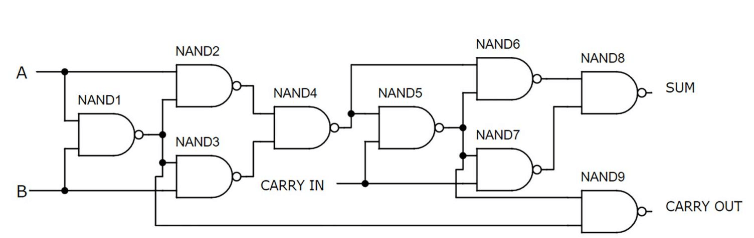
Úplné kladenie pomocou nand brány

Obrázok 7: Celý adder pomocou brány NAND

Táto úplná adder využíva deväť brán NAND, pričom každá brána je vyrobená z dvoch tranzistorov, celkovo 18 tranzistorov.Táto metóda patrí medzi najjednoduchšie a najúčinnejšie spôsoby zostavenia úplného kladu pomocou diskrétnych komponentov.Všetky brány sú zostavené na hornej polovici dosky, zatiaľ čo prepínače zaberajú spodnú polovicu.Funkčnosť obvodu je demonštrovaná so vstupmi A a B zapnuté a prenosom, čo vedie k výstupnej binárnej hodnote 10, čo je ekvivalentná desatinnej 2.

Plná adder s NOR GATES

Obrázok 8: Celá adder s NOR GATES

Toto nastavenie skonštruované s deviatimi ani bránami, z ktorých každá vyžaduje dva tranzistory, používa celkovo 18 tranzistorov.Budovanie úplného addéra s NOR Gates ponúka dobrú alternatívu, ale zahŕňa zložitejšie zapojenie v porovnaní s bránami NAND.Každý tranzistor v bránach NOR je uzemnený, pričom kolektory sú spojené pomocou oranžových prepojkových drôtov, aby sa zabezpečilo čisté a organizované zapojenie.Táto konfigurácia je znázornená so vstupmi A a B aktivovanými a deaktivovanými prepravou, čo vedie k výstupom, kde je prenos aktívny a súčet je vypnutý.

Záver

Počas tohto prieskumu technológie Adder, od základných polovičných addárov po sofistikované návrhy úplného adder, je zrejmé, že tieto komponenty sú základom rozvoja digitálnej elektroniky.Prevádzkové charakteristiky a príklady implementácie poskytovali podčiarknutia všestrannosť a efektívnosť pridaní v rôznych výpočtových nastaveniach.Skúmaním štruktúry a funkcie adders, najmä prostredníctvom ich tabuliek pravdy a charakteristických rovníc, získavame cenné pohľady na ich schopnosti a obmedzenia.Tieto znalosti sú nápomocné pri rozvíjaní navrhovania efektívnejších a rýchlejších výpočtových systémov.V konečnom dôsledku pridania nielen zjednodušujú zložité binárne výpočty, ale tiež umožňujú šírenie technológie v oblastiach tak rozmanitých ako spracovanie údajov, pridelenie pamäte a spracovanie digitálneho signálu.Ako sa vyvíja digitálna technológia, prebiehajúce zdokonaľovanie a inovácie v oblasti návrhu Adder budú naďalej základným kameňom pri vývoji pokročilejších výpočtových architektúr, čím sa zabezpečí, aby tieto základné komponenty zostali v centre digitálneho digitálneho návrhu a implementácie.

Často kladené otázky [FAQ]

1. Čo je obvod s úplným adderom?

Celý adder je digitálny obvod, ktorý pridáva tri binárne bity na výrobu súčtu a výstupu.Je navrhnutý tak, aby zvládol pridanie troch vstupov: dva významné bity a jeden bit prenášania z predchádzajúceho prírastku.To umožňuje jeho použitie v nasledujúcich fázach na pridanie viac-bitových binárnych čísel.

2. Koľko a, alebo, xor v plnom kníhke?

Typický úplný adder obsahuje:

Dve brány XOR na generovanie súčtu.

Dva a brány, ktoré prispievajú k výpočtu vykonávania.

Jeden alebo brána na dokončenie výstupu vykonávania.

3. Čo je vstup na prenos v plnom prúde?

Vstup na prenášanie (CIN) v plnom addéri je prenosný bit z pridania predchádzajúcich nižších významných bitov pri viac-bitovom binárnom pridaní.Umožňuje úplnému kladeniu zvážiť tento predchádzajúci prenos pri výpočte aktuálnej sumy a nového vykonávania.

4. Prečo namiesto polovičného kupca používať úplnú adder?

Namiesto polovičného kaluže sa používa úplná adder, pretože môže pridať tri bity (vrátane nosenia z predchádzajúcich dodatkov), vďaka čomu je vhodný na spoločné reťazenie na pridanie viac-bitových čísel.Polovičnáadra môže pridať iba dva bity a nemá ustanovenie o prenose, čo obmedzuje jeho použitie na najjednoduchšie formy binárneho pridávania bez šírenia postupného nosenia.

O nás

ALLELCO LIMITED

Allelco je medzinárodne slávny na jednom mieste Distribútor služieb obstarávania hybridných elektronických komponentov, ktorý sa zaviazal poskytovať komplexné služby obstarávania a dodávateľského reťazca pre globálny elektronický výrobný a distribučný priemysel vrátane globálnych 500 tovární OEM a nezávislých maklérov.
Čítaj viac